Sophisticated biological methods like single particle tracking and super-resolution imaging rely heavily on particle localization.

Study: Particle Localization Using Local Gradients and Its Application to Nanometer Stabilization of a Microscope. Image Credit: Kashchuk, A. V., et al. ACS Nano 2022

Such approaches need rapid and precise algorithms for particle localization and a microscope that is stable on the nanometer scale.

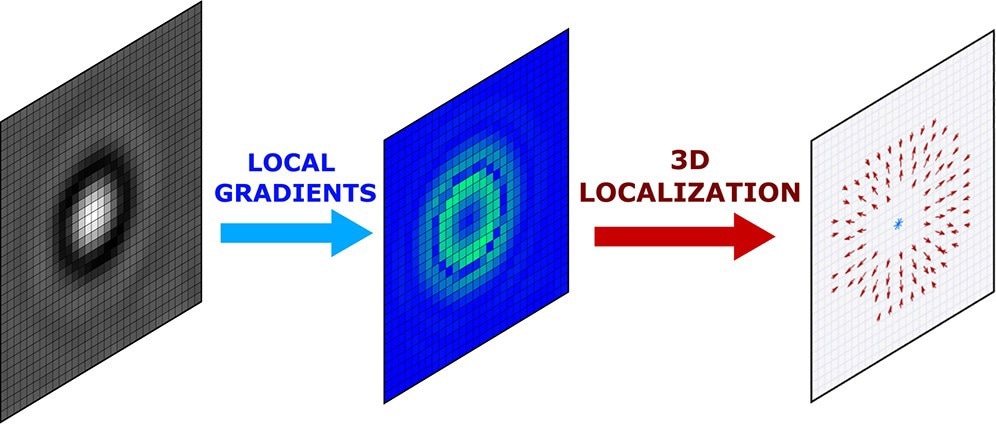
In a paper published in the journal ACS Nano, the researchers showcased a universal approach for 3D localization of labeled as well as unlabeled individual particles using local gradient computation of particle images.

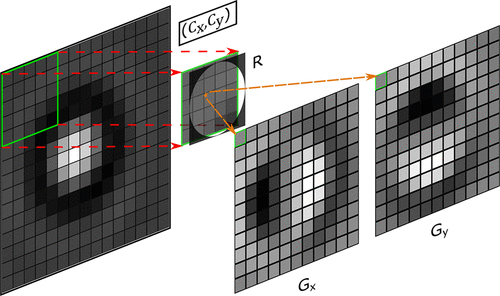
Figure 1. Visualization of the local gradient algorithm. For an m × n image (here 15 × 15) a centroid of a sliding window size K = 2 ⌈r−0.5⌉ + 1 (here 5 × 5 with r = 2.5) is calculated. Each pixel of gradients G_x and G_y is determined as the x (C_x) and y (C_y) coordinates of the centroid, correspondingly, which is calculated relative to the center of the window. The resulting matrices G_x and G_y have the size (m – K) × (n – K). Negative gradient values for images G_x, G_y are represented as darker pixels and positive as whiter pixels. An orange star depicts the centroid. R is a circular mask K × K of radius r.

The Importance of Particle Localization

The localization of microparticles and nanoparticles offers a wide range of applications and is important in several biological and physical processes.

Sophisticated imaging methods like single-molecule localization microscopy (SMLM) have recently emerged that enable the imaging of biological components like viruses, nuclear pores, and cytoskeletal filaments at nanometer-scale resolutions.

SMLM approaches typically use wide-field excitation to attain super-resolution through the localization of single particles.

Active mechanical stabilization in optical microscopy is yet another application where particle localization is needed to determine the position of particles promptly and accurately.

The Role of Drift-Correcting Algorithms

It is impossible to measure protein interactions in a free-running system because of considerable drift that will rapidly transfer the protein molecules outside the interaction zone.

Super-resolution microscopy, which is used to capture a stack of images, encounters a similar issue. In several situations, drift-correcting algorithms may be used post-processing to rectify the displacement of the viewing plane.

These drift-correcting algorithms are particularly successful in the XY-axes. Still, they only function in a narrow range of axial drift because the signal-to-noise ratio of out-of-focus chromophores rapidly reduces, rendering them undetectable.

A feedback mechanism is essential in systems that need nanometer or sub-nanometer stability. A fluorescent marker is usually affixed to a coverslip and then used as a guideline for correction, and the particle’s position must be determined in three dimensions.

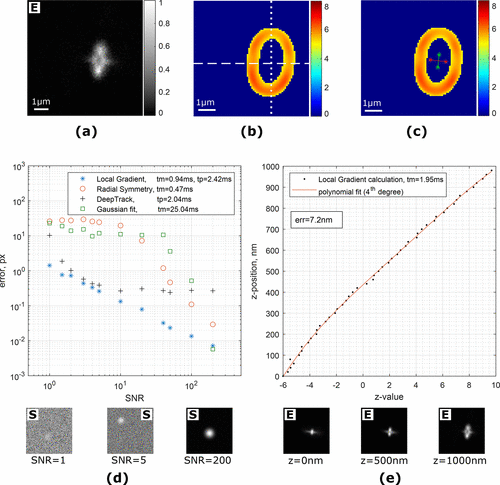
Figure 2. (a) Image of a single fluorescent particle (polystyrene, 0.51 μm) attached to a coverslip. Astigmatism is introduced by a cylindrical lens, and the imaging plane is ≈500 nm above the surface. (b) Magnitude of local gradients. Dashed and dotted lines are showing the top/bottom and left/right split of the local gradient images for z-value estimation, correspondingly. (c) Two axes (green and red lines) are built from the centers of split gradient lines. (d) Comparison of algorithms for localization of a simulated Gaussian-like particle at different noise levels. tm and tp are average execution times in Matlab and Python, correspondingly. Examples of the test images are shown under the plot. (e) z-Value calibration curve in astigmatism-based microscopy. The average error for predicting a z-position of the particle is 7.2 nm. Examples of the test images are shown under the plot. “S” and “E” denote simulated and experimental images.

How Can Nanoparticles Be Localized?

The most popular method for locating an individual particle on a nanometer scale is to use a threshold to choose the brightest pixels of the image and then compute an intensity-weighted centroid.

This approach performs poorly despite its excellent speed and faces various practical difficulties.

In most situations, particles are seen as structures having radial symmetry, and their position may be established as a gradient line crossing.

This method is suitable for testing since it is independent of background level and insensitive to variations in light. Gradient approaches have also been expanded to identify fluorescent particles in three dimensions.

Gradient algorithms offer precise, computationally effective techniques for tracking fluorescent particles and are, therefore, commonly utilized in fluorescence microscopy for quick localization.

What Did the Researchers Do?

In this study, the team presented techniques for the localization of particles and microscope stabilization based on estimations of image intensity local gradients.

The focus of the study was on the application of local gradients in problems of particle localization. A collection of methods was presented for the three-dimensional localization of labeled and unlabeled particles.

The team showed the viability of the local gradient algorithm (LoG) method in XYZ-localization of particles in darkfield and brightfield imaging and for fluorescent particles in astigmatism-based microscopy.

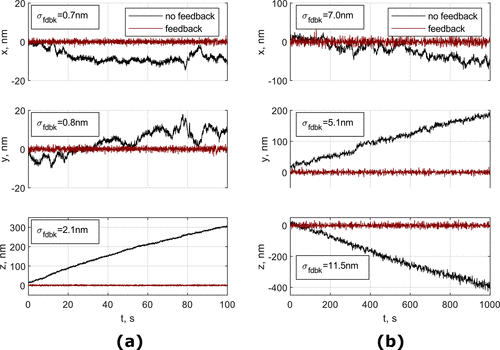
Figure 3. 3D tracking of a spherical silica particle in brightfield microscopy (a) and a fluorescent polystyrene particle in astigmatism microscopy (b) that were attached to the coverslip with feedback system on and off. Inset indicates the standard deviation of the signal with feedback on.

Advantages of Using Local Gradients for Localization

The gradient-based localization algorithms provide several benefits. The low dependency of the local gradients on the background intensity level renders them excellent for particle monitoring under fluctuating or inconsistent lighting.

These approaches may be used to identify particles that are only partly visible in the camera’s field of view. This characteristic might be beneficial when the particle has a restricted field of view or is obstructed by other entities.  

Local gradient algorithms outperform other algorithms in terms of noise resistance and accuracy across the board.

The runtime for mechanical stabilizing systems is a critical parameter for the localization program to achieve a satisfactory feedback frame rate.

Highlights of the Study

The local gradient algorithms were designed mainly for feedback systems which need a quick and accurate estimation of the three-dimensional position of the particle.

The local gradient algorithms offer tools for various microscopy methods, including darkfield, brightfield, and fluorescence microscopy.

The researchers successfully obtained sub-nanometer stability of a microscope stage utilized for protein force spectroscopy.

They demonstrated that a feedback system predicated on the LoG algorithm enhances Z-axis stability and image quality.

Reference

Kashchuk, A. V., Perederiy, O., Caldini, C., Gardini, L., Pavone, F. S., Negriyko, A. M., & Capitanio, M. (2022). Particle Localization Using Local Gradients and Its Application to Nanometer Stabilization of a Microscope. ACS Nano. Available at: https://doi.org/10.1021/acsnano.2c09787

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.